More about Collections

Types Both classes and interfaces represent types. Here are the rules for being a sub/supertype

• If T is a subtype of S, then S is a supertype of T.
• Every type is a sub and supertype of itself.
• If T is a class type and S is an interface type and T implements S, then T is a subtype of S.

Rules for Pointing A variable of a given type can point at any object that is a subtype of the variable's type. For example, you can do these things.

• List<String> ell = new ArrayList<>();
• List<String> ell = new LinkedList<>();
• List<String> ell = new Vector<>();

Super and Sub Interfaces

Suppose S is a set.

A relation R on S is a set of orderd pairs of elements of S

Write xRy if (x,y) ∈ R.

< on numbers

x < x  always false

x < y  then y < x    (antisymmetric)

if x < y and if y < z, then x < z  (this is transitive)

reflexive   xRx for x ∈ S.
symmetric:  xRy guarantees yRx
antisymmetric:  xRy guarantees that yRx is FALSE.
reflexive   xRy guarantees yRx

equivalence: a relation that is symmetric, reflexive and transtive

7

mRn if 7|m - n

reflexive because 7|n - n = 0

If mRn 7| m - n

7 = (m - n)*q
  = (n - m)*(-q)  so 7| n = m   Symmetric!

suppose mRn and nRp

7 | m - n and 7|n = p

m - n = 7*q
n - p = 7*r

add

m - p = 7*(q + r)

7| m - p

mRp  TRANSITIVE


<=

reflexive:  x <= x
transitive x <= y and y <= z  then x < z.

if x < y and y < x, x = y

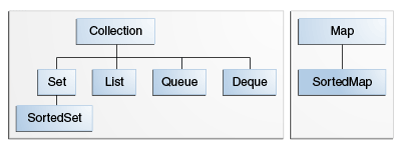
The Java Collections Framework

These interfaces form the "skeleton" of the Collections Framwork. This diagram depicts the subtype relations among the various interfaces.